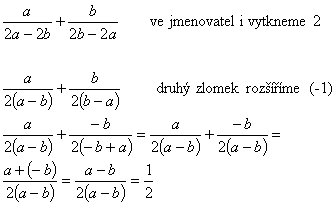




Jste na stránce „na přeskáčku“


Je toho málo. Já si ale na víc netroufám.
Chtěl bych dokázat, že strach z matematiky má stejné kořeny jako strach ze skřítků, netopýrů a jiných temných strašidel.
Také něco málo z moderní historie, která je věcí mého zájmu. Nedělam si však nárok na úplnost
leoblok obsahuje osobní názory autora
 |
Obsah a odkazy |  |
 |
Základní „kuchařka“ |  |
dvěma - sudá čísla
třemi - ciferný součet dělitelný třemi
čtyřmi - poslední dvě číslice dělitelné čtyřmi nebo dvě nuly
pěti - na konci 0 či 5
šesti - dělitelné třemi a současně dvěma
osmi - poslední tři číslice dělitelné osmi, nebo tři
nuly
devíti - ciferný součet dělitelný devíti
deseti - na konci 0
Sčítání zlomků provádíme vhodným rozšířením některých zlomků na společného jmenovatele (zpravidla toho nejmenšího) a sečtením čitatelů. Potom je třeba co nejvíce krátit.
Odčítání se provádí obdobně, avšak čitatele odečítáme.
Násobení zlomků provádíme násobením čitatelů a jmenovatelů mezi sebou. Přitom však vycházejí velké zlomky co do počtu cifer. Proto je možno krátit kteréhokoli čitatele s kterýmkoliv jmenovatelem. Násobení celým číslem si můžeme zapsat jako kdyby toto číslo bylo lomené jedničkou, čímž máme opět dva zlomky.
Dělení zlomků provádíme násobením prvního zlomku převrácenou hodnotou druhého zlomku.
Umocňování zlomků je vlastně násobení tímtéž zlomkem. Děje se to tedy
umocněním čitatele a umocněním jmenovatele.
Např. ![]()
Odmocňování zlomků je analogické umocňování, tedy zvlášť odmocníme čitatele a zvlášť jmenovatele.
Jednoduchá trojčlenka se zapisuje pod sebe a to tak, že souhlasné jednotky musí být pod sebou. Označíme-li známé hodnoty a, b, c, neznámou x, zapíšeme jej takto:
|
|
Jde-li o přímou úměrnost, sestavíme poměry stejným směrem podle šipek (zde směřují obě nahoru, ale mohly by směřovat zrovna také dolů, ale obě musí mít souhlasný směr), tedy
V praxi to píšeme rovnou, kdy nejprve napíšeme x = ——— do čitatele dáme násobení dvou známých v úhlopříčce a do jmenovatele zbylou neznámou.
Jde-li o nepřímou úměru, pak šipky mohou jít tak, jak jsou čárkovaně naznačené, nebo opačně, avšak vždy rozdílným směrem. Pak podle nich opět sestavíme poměr
![]()
V praxi to opět píšeme rovnou, tj. napíšeme x = ——— do čitatele zapíšeme součin známých v řádku bez "x" a do jmenovatele zbylou známou.
V kamenném uhlí je 80 % C, v rašelině jen 6 %. Kolik tun rašeliny obsahuje stejné množství C, jako 2 tuny uhlí?
Úvaha:
Při 80 % C bylo použito 2 t uhlí. Kolik tun bude potřeba rašeliny při 6 % obsahu C? Zápis bude tedy:
80% .................2 t
6 % .................x t
Z další úvahy vyplyne, je-li to přímá či nepřímá úměrnost: Čím více procent bude hornina obsahovat, tím méně ji bude potřeba na stejné množství uhlíku. Tedy úměrnost je to nepřímá. Můžeme tedy psát rovnou zápis:
![]()
Odpověď:
Stejné množství C jako 2 tuny uhlí obsahuje 26,6 t rašeliny.
Složená trojčlenka se řeší stejně jako jednoduchá, avšak množství údajů si rozložíme do několika jednoduchých trojčlenek tím, že se některých členů prozatím nebudeme všímat a zahrneme je teprve do dalšího výsledku, kterého uděláme další, teď už jednoduchou trojčlenku.
Příklad:
Z 30 kg bavlny se utká 240 m látky 1,2 m široké. Kolik metrů látky široké 1,5 m se utká ze 40 kg bavlny?
Řešení:
Nejprve uděláme prvotní zápis
30kg..........240m délka............1,2m šířka
40kg........... x m délka............1,5m šířka
Abychom mohli toto spočítat, musíme si nejprve jednu společnou veličinu odmyslet tím, že ji budeme považovat za neměnnou. Např. si řekneme, že máme nejprve 30kg bavlny. Pak uděláme mezizápis pro jakési x s čárkou (x')

|
Tím můžeme veličiny v kilogramech na okamžik škrtnout a zůstává nám jednoduchá trojčlenka. S tou se snadno vypořádáme stanovením nejprve druhu úměry - čím bude větší šířka látky, tím dostaneme ze stejného množství bavlny menší délku, tedy je to nepřímá úměra a tak podle znalostí z jednoduché trojčlenky rovnou sestavíme zápis
![]()
Dostaneme tedy délku 192m, kterou bychom vyrobili při šířce 1,5m, avšak při použití 30kg bavlny. My ale chceme použít 40kg bavlny. Tedy uděláme novou trojčlenku, kde už nemusíme uvažovat šířku, s kterou jsme počítali dosud, tj. 1,5m.
30kg...............192m délky
40kg................x m délky
Stanovíme úměru - čím více použijeme bavlny, tím větší délku látky vyrobíme, tedy přímá úměra. Zápis bude:
![]()
Odpověď:
Ze 40kg bavlny dostaneme při šířce látky 1,5m délku látky 256m.
Označíme-li a jako základ, n jako exponent, nazýváme n-tou mocninou čísla a číslo an. Pro každé a > 1 platí:
Je-li n > 1, výsledek je větší než a
je-li n = 1, výsledek se rovná a
je-li 1 > n > 0, výsledek je menší než a
je-li n = 0, výsledek je roven 1
je-li n < 0, výsledek je menší než 1
Pro a < 1 platí opačná tvrzení.
Pro a < 0 nejsou v reálném oboru výsledky definovány.
Speciálně lze definovat 0o = 1
Sčítat lze pouze mocniny se stejným základem a stejným exponentem, např.
a5 + a5 = 2a5
obecně
an + an = 2an
Odčítat lze opět pouze mocniny se stejným základem a stejným exponentem, např.
5a3 - 2a3 = 3a3
obecně
5an - 2an = 3an
Násobit lze mocniny se stejným základem a různým exponentem, např.
a3.a2 = a3+2 = a5
obecně
am.an = am+n
Naopak máme-li mocniny různého základu a stejného exponentu, můžeme je sloučit, tedy
a3 .b3 = (ab)3
obecně
an .bn = (ab)n
Obrátíme-li tento zápis, můžeme vyslovit větu: Součin mocnin umocníme, umocníme-li každého činitele
Dělit lze opět mocniny se stejným základem a různým exponentem, např.
a5 : a3 = a5-3 = a2
obecně
![]()
Naopak máme-li mocniny různého základu a stejného exponentu, můžeme je sloučit, tedy
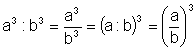
obecně
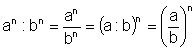
Opět obrátíme-li tento zápis, můžeme vyslovit větu: Podíl umocníme, umocníme-li dělence i dělitele, nebo umocníme-li čitatele i jmenovatele.
Mocninu umocníme jinou mocninou, násobíme-li exponent původní mocniny novým mocnitelem, tedy
(a2)3 = a2 .a2 .a2 = a2+2+2 = a6 = a2.3
obecně
(am)n = amn
Mocninu odmocníme, vydělíme-li exponent původní mocniny odmocnintelem (viz následující stať o odmocninách), tedy
![]()
obecně
![]()
Označíme-li a jako základ (někdy se také nazývá odmocněnec), a
n jako odmocnitel, nazýváme pak n-tou odmocninou čísla a číslo
![]() . Toto číslo je nezáporné
a v reálném oboru má význam jen pro a > 0. Opět můžeme definovat,
že pro a > 1 platí:
. Toto číslo je nezáporné
a v reálném oboru má význam jen pro a > 0. Opět můžeme definovat,
že pro a > 1 platí:
je-li n > 1, výsledek je menší než a
je-li n = 1, výsledek se rovná a
je-li 0 < n < 1, výsledek je větší než a
je-li n = 0, úloha nemá smysl
je-li n < 0, výsledek je menší než 1, ale větší než 0.
Pro 0 < a < 1 opět platí opačná tvrzení a pro a < 0 nejsou v reálném oboru výsledky definovány.
Sčítat lze pouze odmocniny se stejným základem a stejným odmocnitelem. Např.
![]()
obecně
![]()
Odčítat lze opět pouze odmocniny se stejným základem a stejným odmocnitelem. Obecně
![]()
Násobit lze odmocniny o různém základu se stejným odmocnitelem. Výsledkem bude odmocnina ze součinu základů. Bude-li nejprve odmocnitel i základ stejný, dostaneme
![]()
obecně
![]()
Budou-li nyní základy různé a odmocnitelé stejní, dostaneme
![]()
Pozn.:
Násobení odmocnin lze provést i pro jiné případy, jejich vysvětlení je však jednodušší pomocí obecných mocnin, které bude ukázáno v následujícím článku.
Dělit lze odmocniny o různém základu se stejným odmocnitelem.Výsledkem bude odmocnina z podílu základů.
![]()
Pozn.:
Dělení odmocnin lze provést i pro jiné případy, jejich vysvětlení je však jednodušší pomocí obecných mocnin, které bude ukázáno v následujícím článku.
Umocňovat lze jakoukoli odmocninu. Výsledek bude stejný, jako kdybychom umocnili pouze základ. Např.
![]()
obecně
![]()
nebo ještě obecněji
![]()
Odmocňovat můžeme jakékoli odmocniny. Výsledkem bude základ odmocněný součinem odmocněnců.
![]()
obecně
![]()
Řada pravidel, které jsme dosud odvodili, lze nahradit pravidly o počítání s obecnými mocninami a navíc lze vytvořit, zejména pro odmocniny, i další pravidla, která bychom si v původním tvaru těžko pamatovali.
Jde především o záporný exponent, pro který platí, že
![]()
neboť např.
![]()
neboli
![]()
Vidíme, že výsledek je stejný, tedy že rovnost platí.
Zůstaneme-li však u n kladného, můžeme definovat mocninu s převrácenou hodnotou n, tedy 1/n. Platí totiž, že
![]()
Obecnější případ nastane, když n je racionální číslo, tj. obecně číslo ve tvaru zlomku. Pak platí, že
![]()
S touto znalostí můžeme přistoupit k rozšíření řešení násobení odmocnin tak, jak jsme se zmínili v tamější poznámce. Máme-li totiž stejné základy, ale různé odmocnitele, můžeme využít nynějších znalostí a psát
![]()
Podobně můžeme rozšířit otázku dělení odmocnin při stejných základech a různých odmocnitelích.
![]()
Mnohočlen je součet nebo rozdíl několika jednočlenů. Jednočlenem se vždy rozumí součin koeficientu a obecné mocniny neznámé. Přitom koeficient může být určitý, vyjádřený číslovkou, nebo neurčitý vyjádřený písmenem, např. 2, 8, 1/4 jsou určité koeficienty, a, b, k, jsou neurčité. Neznámou, je-li jen jedna, označujeme zpravidla x, takže ji může tvořit x, x2, x5, případně obecná mocnina xn. Tedy jednočlen může mít tvar např. 3x, 5x4, x6, nebo ax, bx3, kxn. Z toho plyne, že mnohočlen může mít tvar např. 3x2 + 2x - 7 a nazýváme jej podle stupně nejvyšší mocniny neznámé, která je v něm obsažena, tj. v tomto případě je to mnohočlen druhého stupně nebo též kvadratický, neboť nejvyšší mocnina neznámé je 2. K danému mnohočlenu dostaneme mnohočlen opačný změníme-li znaménka všech jeho členů. Sčítání či odčítání členů provádíme podle pravidel aritmetiky. Pro přehlednost každý mnohočlen zapíšeme vždy v sestupném pořadí mocnin, tj. od nejvyšší mocniny neznámé po nejnižší, tj. po absolutní člen.
Mnohočleny však mohou být tvořeny několika neznámými, např. x, y, z...
Mnohočlen přičteme k druhému, přičteme-li každý jeho člen, přitom sečíst můžeme jen členy se stejnou mocninou.
(2x2 + 3x + 5) + (4x2 + 7x - 4) = 6x2 + 10x + 1
Závorky v tomto případě nejsou nutné, zde jsme je napsali jen proto, aby oba mnohočleny byly na pohled patrné. Podobně
(2x2y + 3xy2 - 6x + 12) + (4x2y - 7xy2 + 5x - 1) =
6x2y - 4xy2 - x - 11
Mnohočlen odečteme, přičteme-li mnohočlen opačný. Zde hrají závorky nezastupitelnou úlohu a nelze je nikdy vynechat, neboť záporné znaménko před závorkou vždy mění znaménka všech členů v závorce.
(2x2 + 3x + 5) - (4x2 + 7x - 4) = (2x2 + 3x + 5) + (-4x2 - 7x + 4)
Nyní už můžeme závorky zcela vynechat
2x2 + 3x + 5 - 4x2 - 7x + 4 = -2x2 - 4x + 9
Mnohočleny násobíme, násobíme-li každý člen prvního mnohočlenu každým členem druhého mnohočlenu. Zde už jsou závorky zcela neodmyslitelné.
(5x + 3y).(2x + 6y) = 10x2 + 30xy + 6xy + 18y2 = 10x2 + 36xy + 18y2
Jednotlivá znaménka ve výsledku opět dostáváme podle známého aritmetického pravidla, tj.
(+) . (+) = + (+) . (-) = -
(-) . (+) = - (-) . (-) = +
Dělení mnohočlenu mnohočlenem se provádí podobně jako u racionálních čísel. Vznikne-li zbytek, připíšeme jej k výsledku např. jako zb. x, nebo jej vyjádříme jako část dělitele ve tvaru zlomku.
(x2 + 7x + 13) : (x + 4) =
Nejprve dělíme členy s nejvyšší mocninou a podle toho zapíšeme první člen výsledku. Zde je x : x = x, proto zapíšeme do výsledku x a nehledíme na to, co se stane s ostatními členy, hlavně že nám takto jeden člen prvního mnohočlenu ubude. Tento částečný
výsledek hned násobíme s druhým mnohočlenem, což je x . (x + 4) = x + 4x a odečteme od prvního mnohočlenu.
(x + 7x + 13) : (x + 4) = x
-(x + 4x)___
3x + 13
Nyní, stejně jako při dělení dvou čísel, dělíme zbytek druhým mnohočlenem, tj. dělíme (3x + 13) mnohočlenem (x + 4). Zase si všímáme jen nejvyšší mocniny, tj. 3x : x = 3, tedy připíšeme do výsledku +3 a opět tento jednočlen násobíme druhým mnohočlenem, abychom opakovali stejný postup jako v předchozím kroku, tedy
3 . (x + 4) = 3x + 12
(x + 7x + 13) : (x + 4) = x + 3
-(x + 4x)_____
3x + 13
-(3x + 12)__
1
Tím jsme u konce, protože zbytek je menší než druhý mnohočlen a nelze tedy dále dělit. Výsledek tedy je x + 3, zb. 1, nebo, jak bylo uvedeno, výsledek zapíšeme ve tvaru
![]()
V praxi je nezbytné znát aspoň základní mocniny dvojčlenu:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a - b)3 = a3 - 3a2b + 3ab2 - b3
Poznámka:
Lomené výrazy jsou prakticky obecné zlomky. Počítáme s nimi stejně a snažíme se upravit tak, abychom je co nejvíce vykrátili. Často se nám stává, že výrazy ve jmenovateli jsou stejné, avšak s opačným znaménkem. Pak je nejlépe vytknout koeficienty a rozšířit zlomek číslem (-1). Tím se nám změní znaménko buď ve vytknutém koeficientu, nebo v čitateli zbylého výrazu. Typický příklad je tento: