Všechny úhly nad průměrem jsou pravé

Takhle jsme se učili Tháletovu větu my.
Nepatrně názornější znění je:

Všechny úhly vytvořené nad průměrem kružnice jsou pravé.

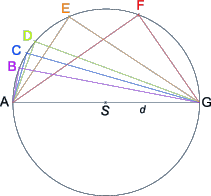    Co se tím rozumí?
    Spojíme-li koncové body průměru s libovolným bodem
    na kružnici, vznikne pravoúhlý trojúhelník jehož
    přeponou je průměr kružnice.

    Jinak řečeno:
    Úhly ABG, ACG, ADG, AEG a AFG na připojeném nákresu
    jsou vždy pravé (=90°)

    Pro úplnost:
    Kružnici, na které leží vrcholy těchto pravoúhlých
    trojúhelníků, říkáme Tháletova kružnice

Typické úlohy
Typické úlohy na Tháletovu větu jsou takové, kde je zadána přepona pravoúhlého trojúhelníku a úhel, který s ní svírá jedna odvěsna. Někdy je místo úhlu zadána délka jedné odvěsny. Řešení je vždy stejné. Úsečku, která představuje přeponu rozpůlíme, ze středu opíšeme kružnici tak, aby úsečka byla jejím průměrem. Pokračujeme podle zadání. Je-li zadán úhel - sestrojíme daný úhel a tam, kde rameno úhlu protne kružnici, je třetí vrchol. Je-li zadaná délka odvěsny, určí nám třetí vrchol průsečík Tháletovy kružnice s kružnicí o poloměru odvěsny. Nezapomeneme, že tyto úlohy mají dvě řešení, každé v opačné polorovině ohraničené přímkou proloženou průměrem Tháletovy kružnice. Může se vyskytnout i modifikovaná úloha, kdy je zadána přepona pravoúhlého trojúhelníku a výška na stranu c. Je to sice spíše středoškolská úloha, ale existují učitelé, kteří ji zadávají i na ZŠ. V tomto případě se vztyčí v libovolném bodu průměru kolmice o délce dané výšky. Koncovým bodem výšky pak vedeme rovnoběžku s průměrem d a tam, kde protne tato rovnoběžka Tháletovu kružnici je třetí bod trojúhelníku. Úloha (takto zadaná) má 4 řešení!